Вписанным в круг называется многоугольник, вершины которого расположены на окружности ( рис.54 ). Описанным около круга называется многоугольник, стороны которого являются касательными к окружности( рис.55 ).
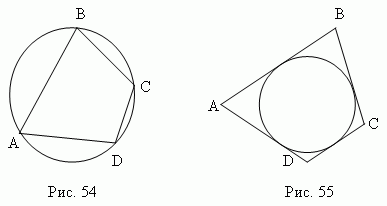
Соответственно, окружность, проходящая через вершины многоугольника ( рис.54 ), называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными ( рис.55 ), называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника это всегда возможно.
Радиус r вписанного круга выражается через стороны a, b, c треугольника:
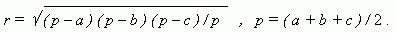
Радиус R описанного круга выражается формулой:
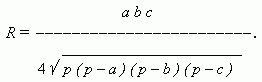
В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба ( квадрата ). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника ( квадрата ). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, если только она равнобочная. |
ну ничего, я что-нибудь придумаю. 